Begin quoted text
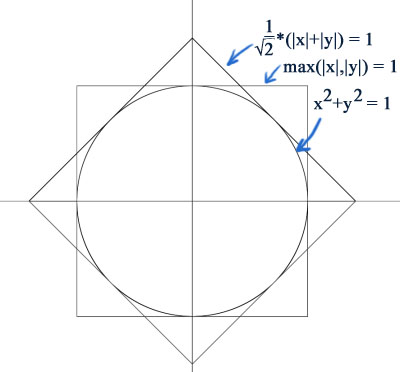
A common application in computer graphics, is to work out the distance between two points as √(Δx2+Δy2). However, for performance reasons, the square root operation is a killer, and often, very crude approximations are acceptable. So we examine the metrics (1 / √2)*(|x|+|y|), and max(|x|,|y|):
Notice the octagonal intersection of the area covered by these metrics, that very tightly fits around the ordinary distance metric. The metric that corresponds to this, therefore is simply:
octagon(x,y) = min ((1 / √2)*(|x|+|y|), max (|x|, |y|))
With a little more work we can bound the distance metric between the following pair of octagonal metrics:
octagon(x,y) / (4-2*√2) ≤ √(x2+y2) ≤ octagon(x,y)
Where 1/(4-2*√2) ≈ 0.8536, which is not that far from 1. So we can get a crude approximation of the distance metric without a square root with the formula:
distanceapprox (x, y) = (1 + 1/(4-2*√2))/2 * min((1 / √2)*(|x|+|y|), max (|x|, |y|))
which will deviate from the true answer by at most about 8%. A similar derivation for 3 dimensions leads to:
distanceapprox (x, y, z) = (1 + 1/4√3)/2 * min((1 / √3)*(|x|+|y|+|z|), max (|x|, |y|, |z|))
with a maximum error of about 16%.
However, something that should be pointed out, is that often the distance is only required for comparison purposes. For example, in the classical mandelbrot set (z←z2+c) calculation, the magnitude of a complex number is typically compared to a boundary radius length of 2. In these cases, one can simply drop the square root, by essentially squaring both sides of the comparison (since distances are always non-negative). That is to say:
√(Δx2+Δy2) < d is equivalent to Δx2+Δy2 < d2, if d ≥ 0
End quoted text
Reference: http://www.azillionmonkeys.com/qed/sqroot.html